FEM01-离散系统数学模型的求解方法

简介

工程分析的一般过程为：将实际工程问题简化为数学模型，然后对数学模型进行求解，得到所需的结果。考虑两大类数学模型：离散系统（Discrete System）模型和连续系统（Continuous System）模型。

离散系统的真实响应（actual response），可以直接由一组状态变量（state variables）的解来描述。其数学模型的控制方程（governing equations）是一组关于状态变量的代数方程（algebraic equations）。直接求解代数方程组，就可以得到准确解（exact solution）。当然，这里指的是数学模型的准确解，并不一定是实际问题的准确解。如果所建立的数学模型是对实际问题的一种近似模型，那么该数学模型的精确解也只是实际问题的近似结果。

连续系统的控制方程，是关于状态变量的微分方程（differential equations）。通常只有一些相对简单的数学模型，才能解出满足所有边界条件的准确解。对于大多数无法求得准确解的数学模型，我们可以采用数值方法（numerical procedures）将连续的微分方程转换为离散的代数方程组，求解得到近似解（approximate solutions）。常用的方法有：有限单元法（FEM，Finite Element Method）和有限差分法（FDM，Finite Difference Method）。

FEM Vs FDM mesh

右图展示了有限元法和有限差分法两者在网格方面的差异。

有限元法，可以针对不同类型的单元采用与之对应的形状函数来近似描述，适应性更好，结果更加精确，在工程上广泛使用。但对于复杂模型，计算量大，对计算机配置要求高。

有限差分法，基于欧拉法实现，采用差分近似代替求导，算法简单，计算速度快。

求解离散系统的一般步骤

  1. System idealization: 理想化实际问题，将分析对象离散为一个个单元，构建离散系统。
  2. Element equilibrium: 确定状态变量，分别对每个单元建立关于状态变量的平衡方程。
  3. Element assemblage: 建立单元之间的连接关系，对所有单元进行组装，联立方程组。
  4. Calculation of response: 求解方程组，得到系统的响应。

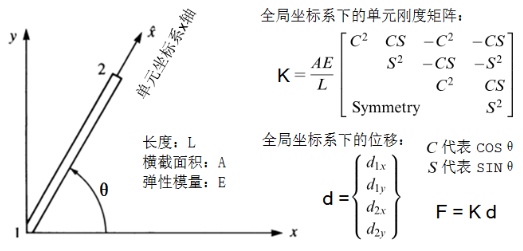
注意：在对刚度矩阵进行组装时，应确保所有单元的刚度矩阵在统一的全局坐标系下定义。如果单元坐标系与全局坐标系不一致，需要进行转换。如图所示的杆单元，与全局坐标系的夹角为θ。在全局坐标系中的单元刚度矩阵如下：

FEM01_transformation.png 桁架单元刚度矩阵坐标转换

例题

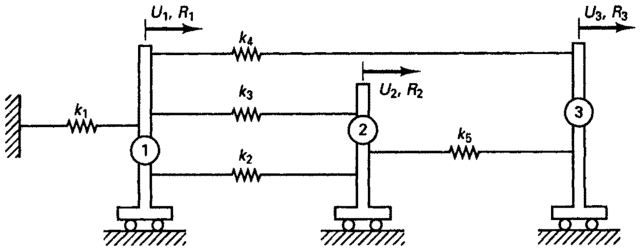
例1.1：图示的系统包含三个刚性小车和连接弹簧，弹簧刚度分别为k1，k2，……k5，小车受到的载荷分别为R1，R2，R3，求各个小车的位移和各个弹簧的力。

FEM01_1_spring.png 弹簧模型有限元法

以矩阵形式，分别写出每个单元的平衡方程。Fi(j) 表示 j 号单元在 i 号节点上的力。

然后，组装所有单元的刚度矩阵，得到总体刚度矩阵。

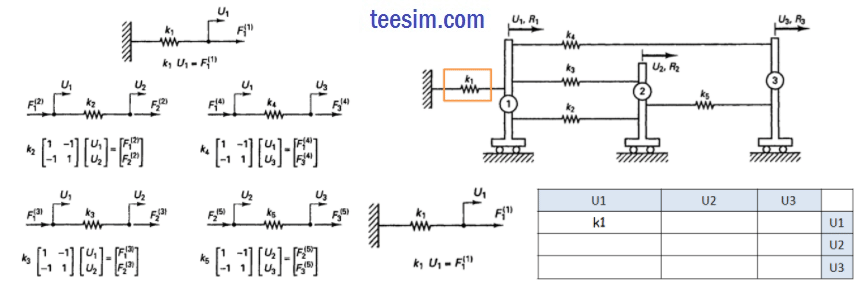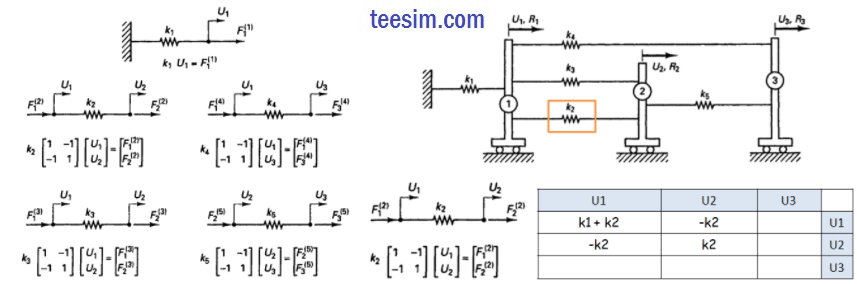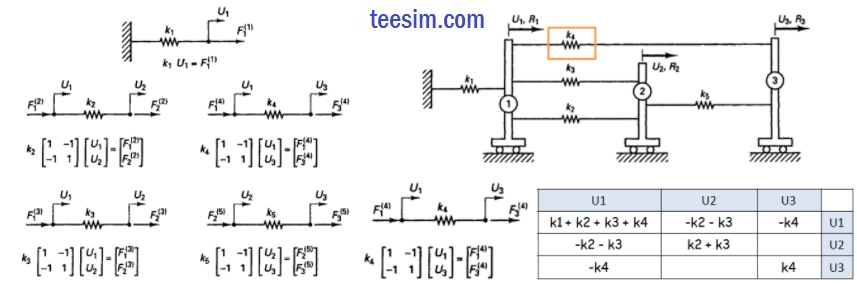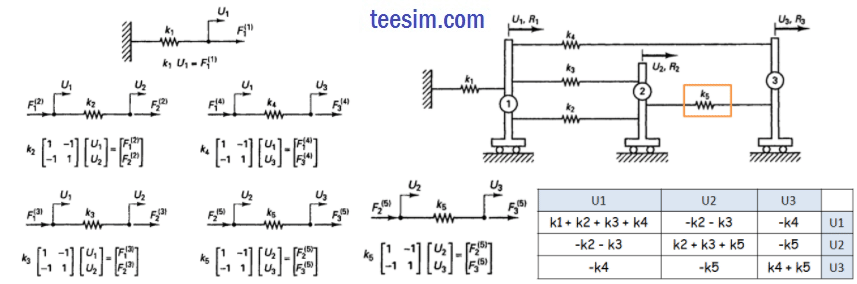
FEM01_assem_matrix.gif 组装刚度矩阵

i号节点上所有单元的合力，等于该节点受到的外力Ri；得到代数方程组，求解可以得到各个节点的位移。再根据单元平衡方程，求出每个弹簧的力。该方法，称为“直接刚度法”（direct stiffness method）。

FEM01_stiffness_method.jpg 直接刚度法

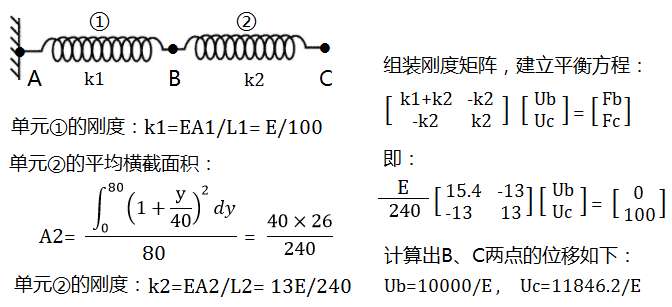
例1.2：如图所示的变截面杆，弹性模量为E，左端固定，右端受到R=100N的力，求B、C两点的位移。

FEM01_2_bar.png 变截面杆有限元解法

将杆的两段离散为两个弹簧单元，分别计算每一段杆的轴向刚度k=EA/L，作为弹簧刚度。注意：对于变截面的杆，计算刚度时应采用平均截面积。离散后的模型，可以采用上一个例题的方法进行求解。

FEM01_2_discrete.jpg 变截面杆的离散模型

例1.3：如图所示的桁架结构，已知各个杆的长度、弹性模量和横截面积，约束和载荷如图。求各节点的位移和约束点的支反力。

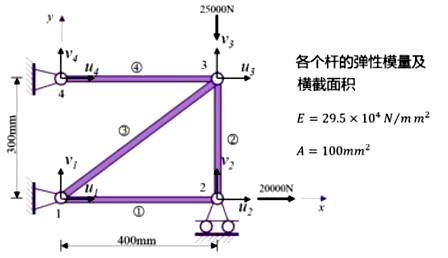
FEM01_3_truss.jpg 桁架模型有限元法

桁架（truss）的特点是，等截面杆，两端铰接，只能传递轴向拉压载荷，无法传递弯矩。因此每个节点只有移动自由度，不需要考虑转动自由度。每个单元也只需要考虑轴向拉压刚度。

这里采用Excel进行矩阵运算。首先，写出各个单元的刚度矩阵。

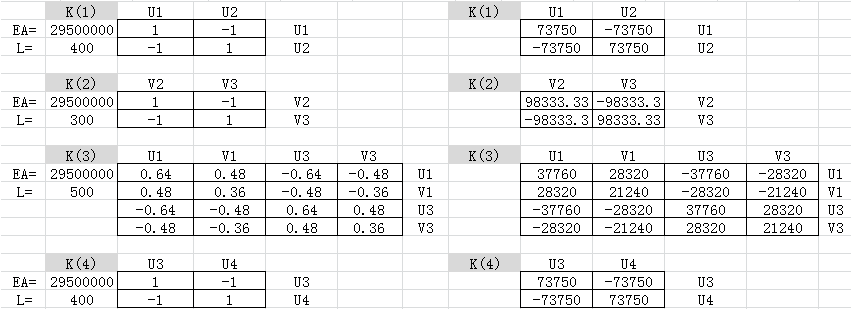
FEM01_3_elem_stiffness.png 桁架模型单元刚度矩阵

然后，组装得到结构的整体刚度矩阵。并采用消元法，将位移为零的项所对应的行和列划掉。

FEM01_3_assem_matrix.png 桁架模型组装刚度矩阵

对于消元后简化的刚度矩阵K，求出它的逆矩阵K-1，然后用K-1乘以载荷向量F，得到位移结果。

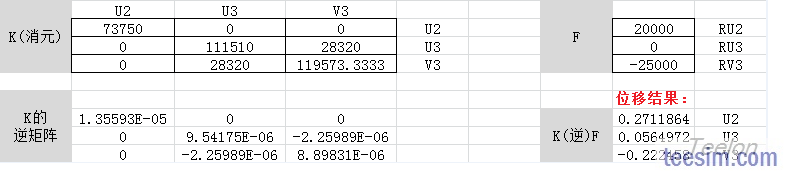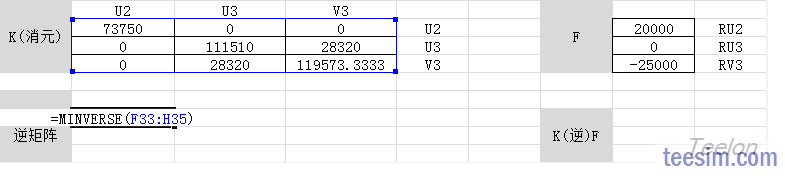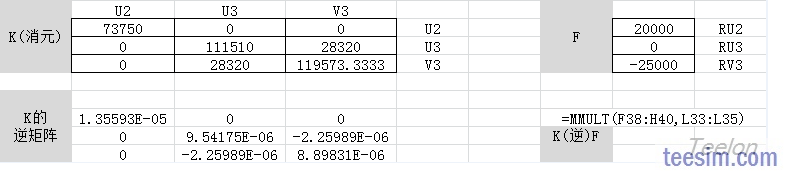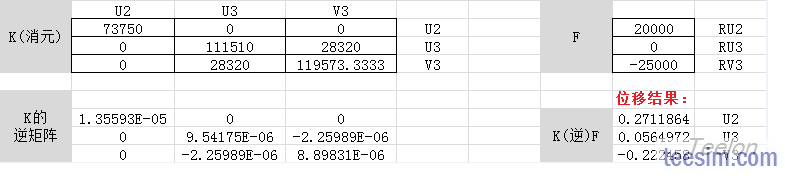
FEM01_3_matrix_operation.gif Excel矩阵运算

最后，根据F=KU，可以求出各个约束点的支反力。

FEM01_3_reaction.png 约束反力

总结

例1.1介绍了采用直接刚度法求解离散系统的步骤。
例1.2的分析对象虽然是连续系统，但这里将其简化为离散系统进行求解。
例1.3涉及单元刚度矩阵的坐标系统一和矩阵运算，加深对直接刚度法求解过程的理解。

Reference:

  • www.simtec-inc.com/fem_vs_fdm.htm
  • A First Course in the Finite Element Method by Daryl L. Logan
  • Finite Element Procedures by Klaus-Jürgen Bathe 轩建平 译
  • 有限元基础教程 by 曾攀