FEM02-连续系统的微分方程

简介

求解连续系统的基本步骤与离散系统类似，两者的主要区别在于：离散系统是针对离散的单元建立平衡方程，而连续系统是从微分的角度关注微元的平衡关系，并结合本构方程建立微分方程。连续系统的微分方程，必须在系统的整个域（domain of the system）上都能得到满足，也称为系统的控制方程。其解应满足边界条件，对于动态问题，还应满足初始条件。

微分方程

从数学的角度，可以将微分形式的控制方程进行分类。考虑以下关于x，y的一般二阶偏微分方程（Partial Differential Equation，简称PDE）：

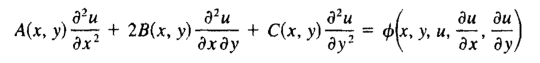
其中，u是未知的状态变量。根据系数A，B，C之间的关系，可将偏微分方程分为椭圆方程（elliptic），抛物线方程（parabolic）和双曲线方程（hyperbolic）：

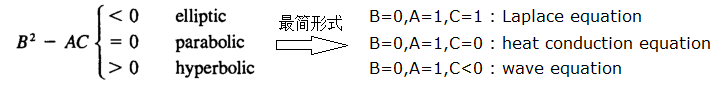
注意：如果微分方程中第二项的系数，是B而不是2B，则判别式应为B²-4AC而不是B²-AC。

这样分类的好处在于：三种类型的微分方程，分别对应三种不同类型的物理问题。这三种类型的最简形式，分别是拉普拉斯方程（Laplace equation）、热传导方程（heat conduction equation）和波动方程（wave equation）。下面用三个例子，来解释这三种微分方程所适用的物理问题。

例题

例2.1：如图所示的二维理想化大坝，立于可渗水的土壤上。

例2.2：如图所示很长的平板，初始温度为θ_i。在x=0的表面突然受到恒定的均匀热流输入，在x=L的表面温度保持θ_i不变，平行于xz平面的表面绝热。

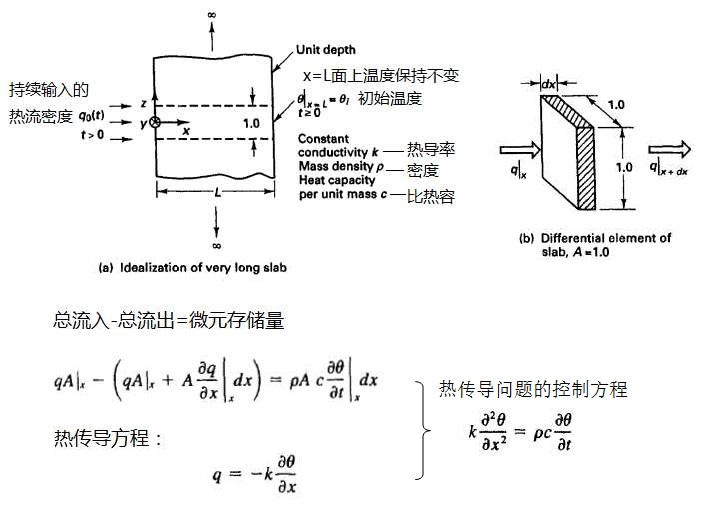
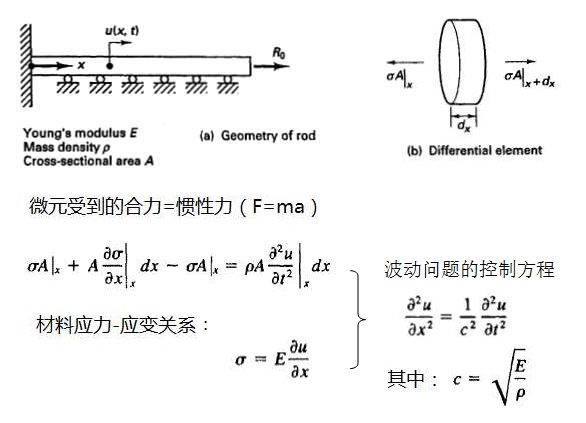
例2.3：如图所示杆，初始状态静止，自由端突然受到载荷R(t)作用。

总结

在椭圆问题中（例2.1），未知状态变量（或其法向导数）在边界上是给定的，我们称之为“边值问题”（boundary value problems）。椭圆微分方程，一般控制系统的稳态响应（steady-state response）。

与椭圆方程相比，抛物线方程（例2.2）和双曲线方程（例2.3）还将时间作为独立变量，因此是传播问题，又称为“初值问题”（initial value problems）。如果忽略与时间有关的项，则例2.2和例2.3的抛物线方程和双曲线方程就会变成椭圆方程；这时，初值问题就变成了具有稳态解的边值问题。

Reference:

• Finite Element Procedures by Klaus-Jürgen Bathe 轩建平 译
• A First Course in Finite Elements by Jacob Fish & Ted Belytschko