FEM06-加权余量法

简介

在“FEM04-里玆法（Ritz Method）”中，需要写出总势能的表达式，而不必建立控制方程。对于有些问题，可能已经建立了控制方程（ODE/PDE），如何直接对微分控制方程进行近似求解？本文将介绍一类通用的方法——加权余量法（ Weighted Residual Method ）。加权余量法主要有以下三个步骤：

  1. 选择满足边界条件的试函数（包含基函数和待定系数）。
  2. 将试函数代入控制方程计算残差。由于试函数不是准确解，将会产生残差或余量（Residual）。
  3. 用权函数（weight function）乘以上一步中的余量，并在定义域内求积分；该积分等于零，得到关于待定系数的代数方程，解方程可以求出待定系数。

加权余量法

考虑以下微分方程所描述的稳态问题：

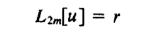
FEM06_differential_formula.png 稳态问题的微分方程

其中L2m是线性微分算子，u是需要求解的状态变量，r是强迫函数（已知项，不包含状态变量）。问题的解还应满足边界条件：

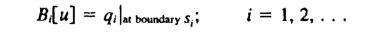
FEM06_boundary_condition.png 边界条件

  1. 假设解的形式为（试函数）：

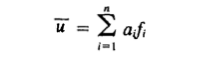
    2. FEM04_trial_function.png 试函数，多项式函数

    其中，fi是线性无关的基函数，ai是待定系数。选择合适的基函数，使试函数满足所有边界条件。

  2. 计算残差：

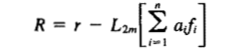
    3. FEM06_residual.png 残差或余量

    对于准确解，残差肯定是零。良好的近似解，意味着残差R在定义域内所有的点上都很小。

  3. 用权函数w乘以残差R，使其在定义域内的积分为零。这样就使得定义域内的残差在某种加权平均的意义上等于零。

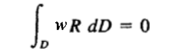
    4. FEM06_WRM.png 加权余量法

以上就是加权余量法的求解过程。根据所选的权函数不同，加权余量法可以分为：配点法（Collocation method），子域法（Subdomain method），最小二乘法（Least squares method）和伽辽金法（Galerkin method）等。

配点法

首先从定义域内取一些点，取点的数量取决于试函数中未知待定系数的个数。然后，直接让残差在这些点上等于零。取点的位置可以是任意的，一般情况下均匀布点比较合适，但也可以根据分析需求适当调整。

子域法

子域法的权函数等于1，即直接在定义域内对残差求积分等于零。通常把整个定义域分成若干个子域，然后分别对每个子域进行积分。

最小二乘法

目标：残差平方的积分，关于ai是最小的。即：R2在定义域内积分，然后对ai求偏导等于零。

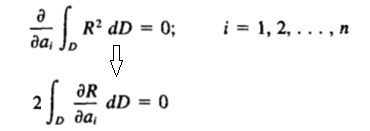
FEM06_least_square1.png 最小二乘法

对应的权函数为：∂R/∂ai；有多少个待定系数ai，就有多少个权函数wi。

将残差的表达式代入，权函数也可写作L2m(fi)：

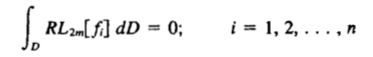
FEM06_least_square2.png 最小二乘法

伽辽金法

与最小二乘法类似，只是把权函数中残差的偏导数∂R，替换为试函数的偏导数∂ū。权函数为：∂ū/∂ai（试函数ū对ai求偏导），实际上就是基函数fi。因此，伽辽金法的权函数，就是试函数的基。

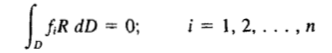
FEM06_galerkin.png 伽辽金法

例题

考虑以下微分方程，分别采用配点法，子域法，最小二乘法和伽辽金法进行求解。

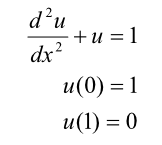
FEM06_example.png 加权余量法例题

求解过程详见：www.me.ua.edu/me611/f04/pdf/mwr.pdf，这里不再赘述。

针对这个例子，注意以下两点：

  1. 微分控制方程最高阶导数的阶次是2m阶，计算残差R时必须将试函数代入控制方程。因此，所选的试函数也必须2m阶（或以上）可导。本例中，m=1。
  2. 试函数必须满足所有边界条件。本例中的所有边界条件都是本质边界条件（最高阶导数为m-1阶），比较容易构造满足这类边界条件的试函数。如果边界条件也包含自然边界条件（含m阶或更高阶次的导数），要让试函数也满足自然边界条件就不太容易了。

伽辽金法的实际应用

在“FEM04-里玆法（Ritz Method）”的例题中，既包含本质边界条件，又包含自然边界条件。

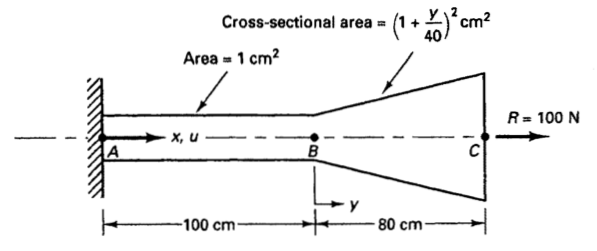
FEM01_2_bar.png 变截面杆稳态问题

控制方程为：

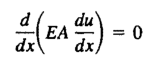
FEM06_governing_equation.png 控制方程

本质边界条件为：

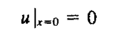
FEM06_essential_BC.png 本质边界条件

自然边界条件为：

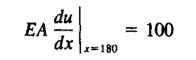
FEM06_natural_BC.png 自然边界条件

下面尝试用伽辽金法来求解该问题。

  1. 构造试函数（满足所有边界条件）：

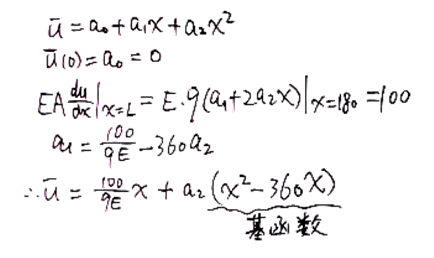
    2. FEM06_galerkin1.png 试函数

  2. 计算残差：

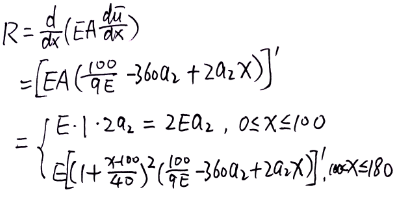
    3. FEM06_galerkin2.png 试函数

  3. 残差加权积分：

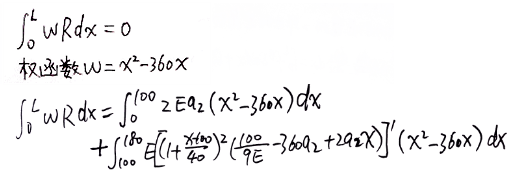
    4. FEM06_galerkin3.png 试函数

该方程比较复杂，不太容易求解。造成它这么复杂的原因，主要还是前面提到的两点：(1)试函数必须2m阶可导；(2)试函数必须满足所有边界条件。在“FEM04-里玆法（Ritz Method）”中介绍的里兹法，试函数只需m阶可导，而且只需满足本质边界条件，不必满足自然边界条件。相比之下，里兹法的试函数更加灵活，具有更大的函数空间。

那么问题来了：前面忙活了半天，详细介绍了各种加权余量法，而真正遇到实际问题的时候，发现它根本不实用，还不如里兹法好用。就好比孙悟空大闹东海，终于取得秒天秒地秒大海的定海神针，却发现这家伙又大又丑，那我要这铁棒有何用？别急，现在就差一句咒语，就能让这根铁棒完美变身。它就是——“虚位移原理”（详见“FEM05-虚位移原理”）。它可以化腐朽为神奇，将强形式变为弱形式，降低对试函数的要求，使得试函数拥有更大的函数空间。

现在，我们用“虚位移”的方式来打开“伽辽金法”。

首先，用虚位移原理来描述问题。

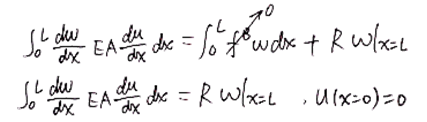
FEM06_weak_galerkin.png 虚位移原理

其中，w既是虚位移，又是权函数。（此处是关键）

本质边界条件为：

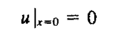
FEM06_essential_BC.png 本质边界条件

同时，在本质边界条件处，虚位移应等于零：

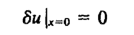
FEM06_weak_galerkin0.png 虚位移为零

自然边界条件不需要再写了，因为它已经包含在虚位移原理中。

经过此番变化，试函数只需m阶可导（m=1），边界条件也只剩下本质边界条件。这样，加权余量法就可以选择和里兹法一样的试函数了。

然后，运用伽辽金法进行求解。

  1. 构造试函数：

    2. FEM04_trial1.png 试函数为一次函数

  2. 虚位移原理的方程中，已经包含了权函数。伽辽金法的权函数是试函数的基，直接将权函数代入该方程即可求出待定系数uB和uC。

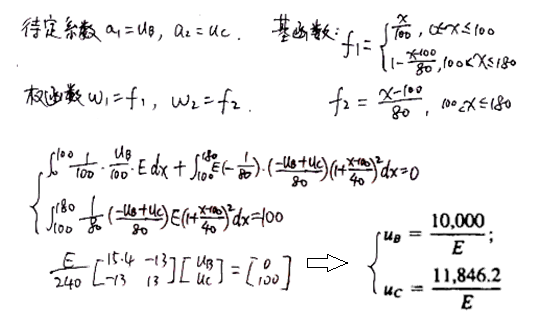
    3. FEM06_weak_galerkin1.png

Reference:

  • Finite Element Procedures by Klaus-Jürgen Bathe 轩建平 译
  • A First Course in Finite Elements by Jacob Fish & Ted Belytschko