FEM08-广义坐标有限元

简介

“FEM07-从虚位移原理到有限元”介绍了有限元法求解线性结构问题的基本流程，该方法的关键在于构造位移插值矩阵H。本文以平面应力单元为例，介绍运用广义坐标（Generalized Coordinate）构造位移插值矩阵H的方法以及有限元求解过程。

例题

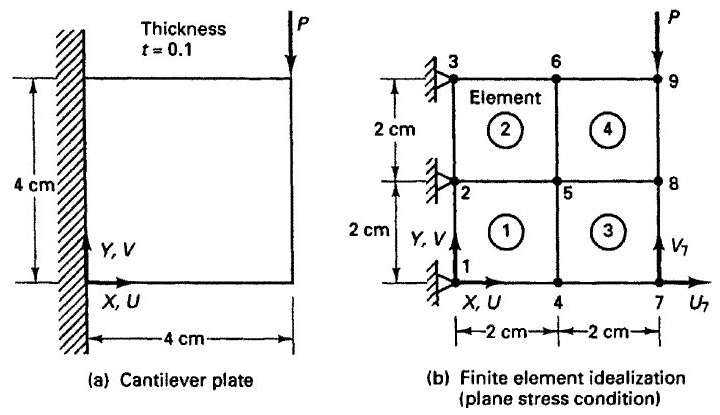
如图所示的悬臂板处于平面应力（plain stress）状态，划分为4个四边形单元。试建立2号单元的位移插值矩阵H、应变-位移矩阵B和材料属性矩阵C。

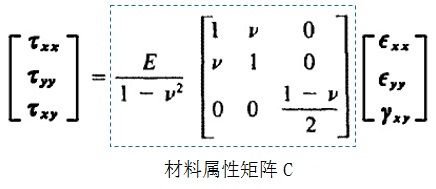
平面应力状态，只包含τ_xx, τ_yy, τ_xy三个应力分量。对于各向同性线弹性材料，其应力应变关系满足广义胡克定律，得到材料属性矩阵C.

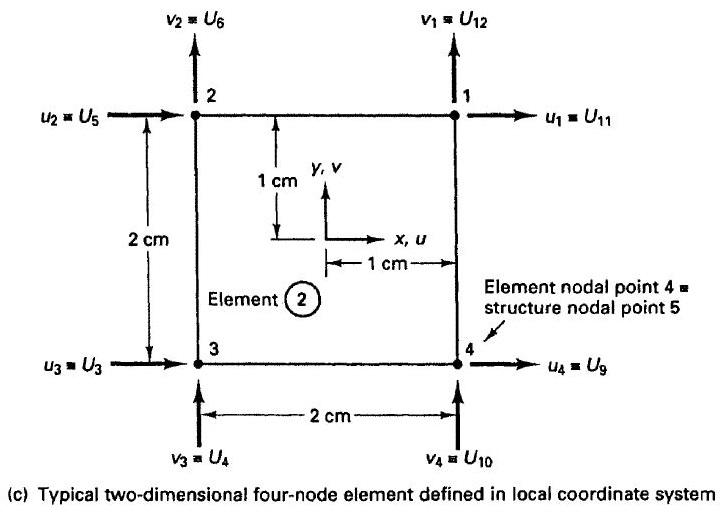
2号单元内部的位移分布，由插值矩阵H乘以节点位移U得到。

只有6、3、2和5这四个节点的位移会影响2号单元内的位移分布。为了便于计算，以单元中心为原点建立单元局部坐标系，自由度方向与全局坐标系一致，并对该单元的节点重新编号，依次为1、2、3和4。那么，2号单元的节点位移Û可写作：

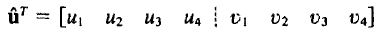
在单元局部坐标系中，采用如下多项式函数来构造单元内的位移函数u(x, y)和v(x, y)：

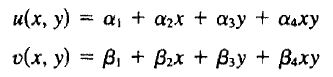
其中的未知系数α1,……,α4, β1,……,β4称为广义坐标，将它们写成向量的形式：

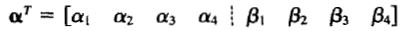
单元内的位移函数可用矩阵描述：

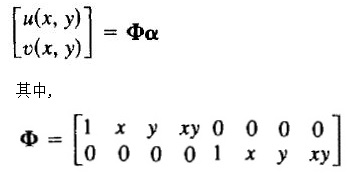
单元的四个节点处，都应满足位移函数，将这四个节点的坐标分别代入位移函数，得到：

u1=u(1,1)=α1+α2+α3+α4; v1=v(1,1)=β1+β2+β3+β4

u2=u(-1,1)=α1-α2+α3-α4; v2=v(-1,1)=β1-β2+β3-β4

u3=u(-1,-1)=α1-α2-α3+α4; v3=v(-1,-1)=β1-β2-β3+β4

u4=u(1,-1)=α1+α2-α3-α4; v4=v(1,-1)=β1+β2-β3-β4

写成矩阵形式，即：

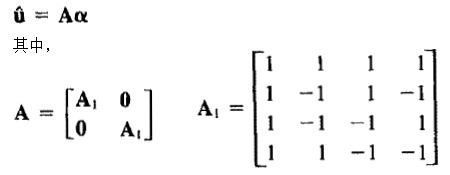
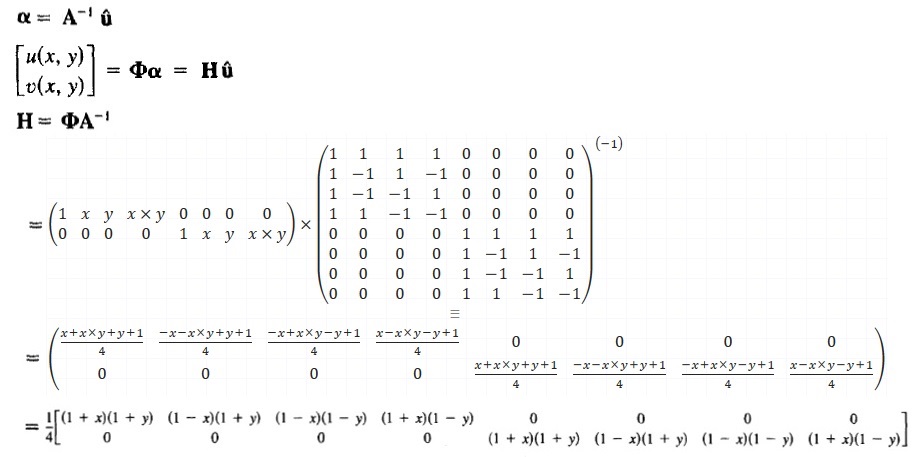
将广义坐标用节点位移表示，代入位移函数，可以求出位移插值矩阵H：

平面应力状态的三个应变分量为：ε_xx, ε_yy, γ_xy：

应变-位移矩阵B可以由H推导出来。

最后再把单元节点的局部自由度和全局自由度对应起来，即可写出2号单元关于全局自由度的位移插值矩阵H和应变-位移矩阵B。

给定：杨氏模量E =2700000，泊松比ν=0，板厚t = 0.1，载荷P=100；求各个节点的位移。

对于该网格模型中的任何一个单元m，分别建立元局部坐标系。将其节点从右上角开始，沿逆时针方向依次编号：1、2、3和4。每个单元的节点位移向量都可记为：

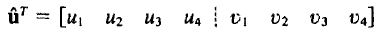
ν=0，材料属性矩阵C：

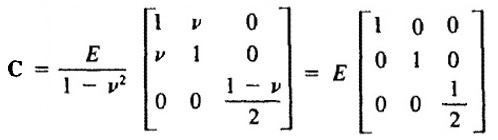
每个单元的刚度矩阵K(m)：

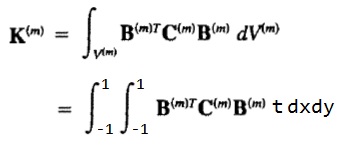
其中B^TCB矩阵计算如下。

该矩阵各项元素分别在单元域内对x和y进行双重积分，可以求出单元刚度矩阵。求积分可以参考Wolfram|Alpha网站中的小程序：“https://www.wolframalpha.com/widgets/view.jsp?id=f5f3cbf14f4f5d6d2085bf2d0fb76e8a”

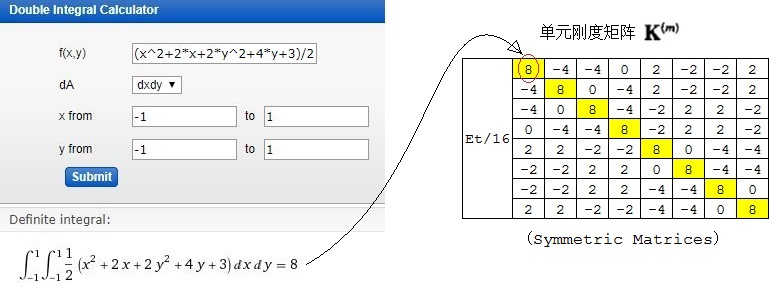
由于本例中每个单元的几何尺寸、材料属性和插值函数都一样，所以每个单元刚度矩阵也都是一样的。只不过每个单元节点相关的全局自由度不同。各个单元刚度矩阵及对应的自由度如下：（省略了常数Et/16）

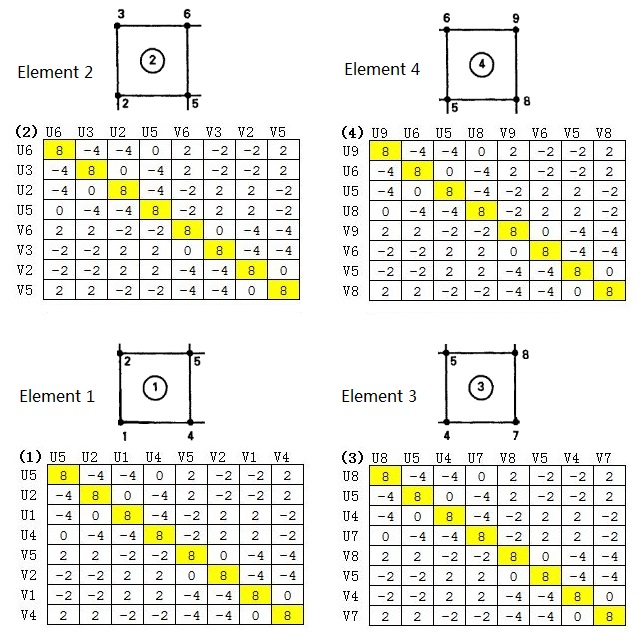
全局自由度中与某个具体单元无关的部分用0补充，得到每个单元关于全局自由度的刚度矩阵。

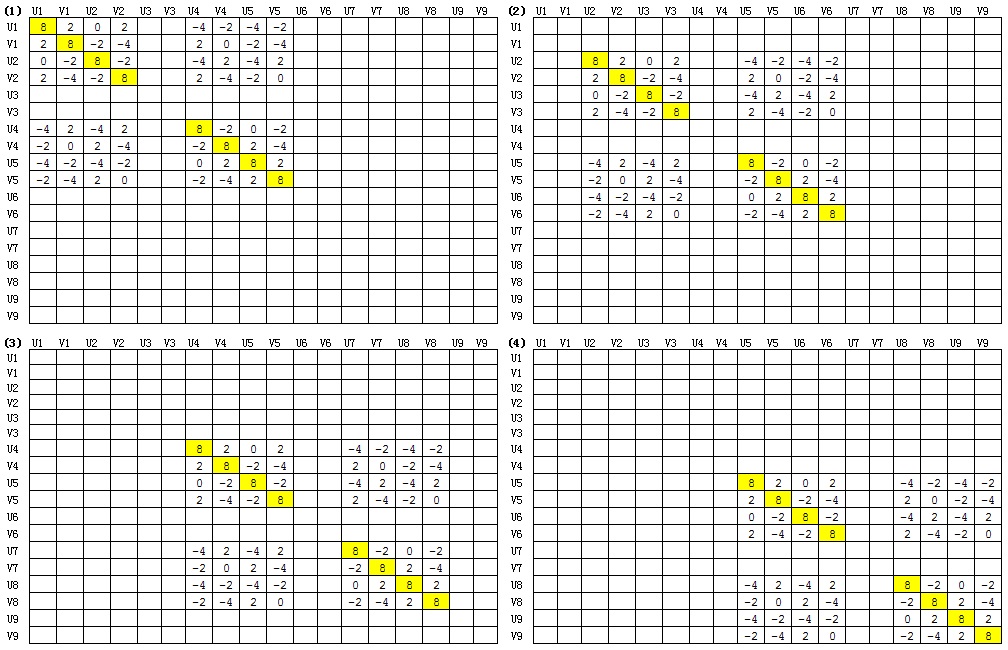
然后进行组装，得到总体刚度矩阵。

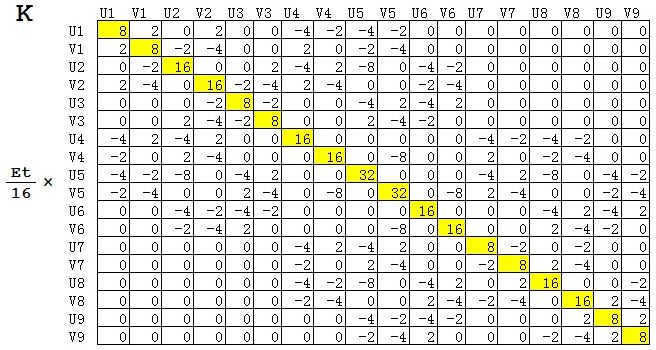
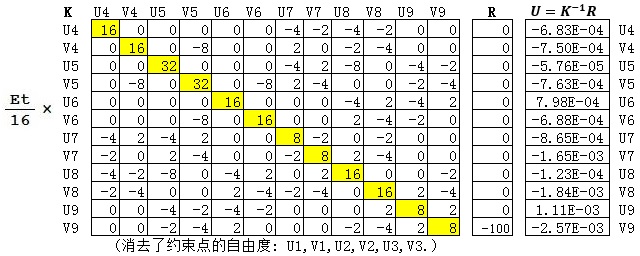
根据约束条件，消去节点1、2、3对应的所有自由度。根据载荷条件，写出载荷向量R。根据KU=R，即可求出各个节点的位移。

Reference:

• Finite Element Procedures by Klaus-Jürgen Bathe 轩建平 译
• A First Course in Finite Elements by Jacob Fish & Ted Belytschko