FEM09-非协调单元
简介
在“FEM08-广义坐标有限元”中,介绍了将一次函数作为试函数,采用标准形式的基于纯位移变量的单元(standard pure displacement-based element)进行有限元计算的方法。该方法可以有效处理很多问题,但对于弯曲变形和不可压缩介质的分析,不是很有效。在弯曲问题中,该方法存在剪切自锁(shear locking);在不可压缩问题中,该方法存在体积自锁(volumetric locking)。这两种自锁,是由于所选的试函数或位移变量不能有效描述单元的变形而造成的。本文介绍采用基于位移的非协调单元解决剪切自锁问题的方法。(体积自锁问题,以后再做介绍。)
剪切自锁
根据“FEM08-广义坐标有限元”中一阶四边形平面应力单元的位移函数,用广义坐标表示各个应变分量:

观察应变的表达式,可以发现以下两个问题:
1、正应变εxx只与y有关,与x无关。因此,它无法描述εxx随x坐标变化的情况。
2、当α4≠0,正应变εxx与y坐标成正比。这种情况,符合纯弯曲状态梁横截面的正应变在垂直于中性层的方向上的分布规律。但另一方面,由于α4≠0,此时切应变γxy≠0,与纯弯曲状态切应变为零的事实不相符。
下图显示了纯弯曲状态应该表现出的变形模式。
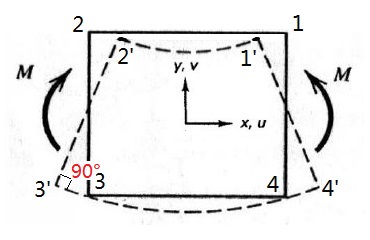
节点1、2、3、4分别移动到1'、2'、3'、4'位置。各个位移分量之间的关系如下:
u1=u3, u2=u4, u1=-u4;
v1=v2, v3=v4, v1=-v4;
将这四个节点的坐标分别代入位移函数,得到:
α1=α2=α3=0; β1=β2=β4=0.
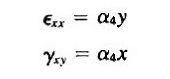
可以看出:当α4≠0,正应变εxx与y坐标成正比;而切应变γxy≠0.
这种单元在纯弯曲状态的变形模式如下:
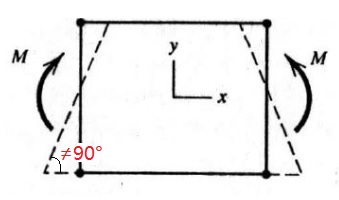
原本互相垂直的单元边,不再保持垂直,产生了剪切应变(γxy≠0);而实际上纯弯曲状态是没有剪切应变的(γxy=0)。这种现象称为剪切自锁。剪切自锁是一种错误,它会使结构抵抗弯曲变形的能力(抗弯刚度)大于实际值,造成计算出来的位移偏小。
The additional shear stress in the element (which does not occur in the actual beam) causes the element to reach equilibrium with smaller displacements, i.e., it makes the element appear to be stiffer than it actually is and gives bending displacements smaller than they should be. 单元中额外产生的剪切应力(实际不应该产生),使其只需要更小的位移就能达到平衡。这会使单元刚度更大,弯曲变形的位移比实际更小。
非协调单元
很显然,如果采用试函数为二次函数的二阶单元,就可以解决前面描述的剪切自锁问题。但毕竟增加单元阶次,会带来计算量的增加,降低效率。于是,有限元的先驱者们,提出了非协调模式的单元。它具有和标准一阶单元相当的计算效率,同时又显著改善了剪切自锁问题。
非协调模式的四边形平面应力单元的位移函数如下:
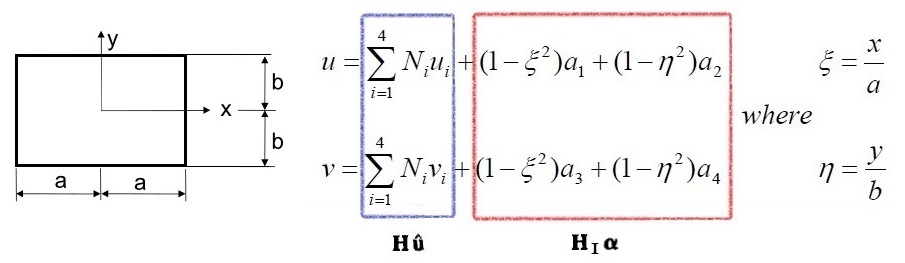
可以看到,它是在标准形式的位移函数后面,多了个“尾巴”(HIα)。
参考“FEM08-广义坐标有限元”,以矩阵形式写出非协调模式单元的应变:
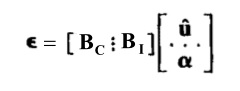
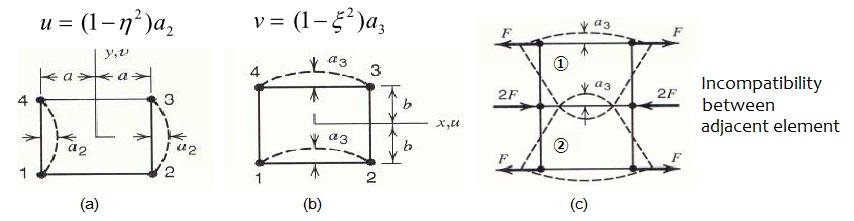
其中,BC是标准的应变-位移矩阵(协调模式),BI是非协调模式中应变-位移矩阵的增加项,u是各个节点自由度对应的位移,α是非协调模式增加的自由度(αT=[ a1,a2,a3,a4 ])。这些额外增加的自由度,在相邻单元之间是不协调的,所以称为非协调模式。如下图所示,(a)表示仅a2不为零时的变形模式, (b)表示仅a3不为零时的变形模式,(c)表示相邻两个单元之的a3自由度是相互独立的(不共有),表现出非协调性。
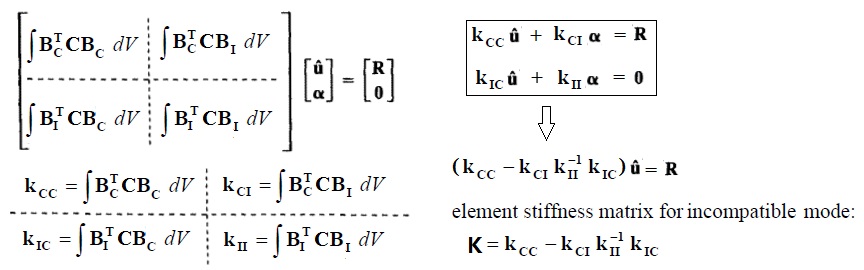
根据虚位移原理,写出平衡方程。由于增加的自由度是单元内独有的自由度,不会改变外载荷的分布。因此,载荷向量中对应于α的项直接用0补齐即可。这样就可以得到非协调模式单元的刚度矩阵K。后面的求解过程,和“FEM08-广义坐标有限元”中介绍的一样,不再赘述。
例题
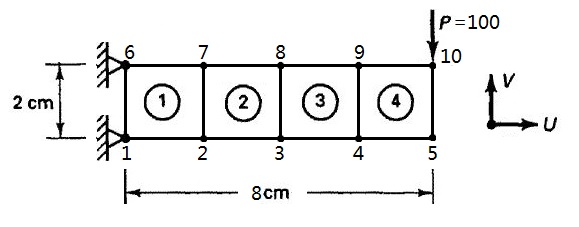
如图所示的悬臂板,板厚t=0.1,划分4个正方形平面应力单元。每个单元边长为2,端部载荷P=100,杨氏模量E =2700000,泊松比ν=0. 分别用协调模式和非协调模式的单元求解各个节点的位移。
协调模式的单元刚度矩阵,和“FEM08-广义坐标有限元”中的一样。对于非协调模式,需要先写出BC和BI,再根据前面介绍的方法写出单元刚度矩阵。
本例中,a=b=1,BC和BI如下:
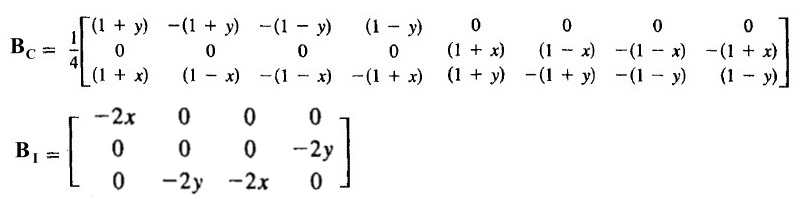
计算单元刚度矩阵:
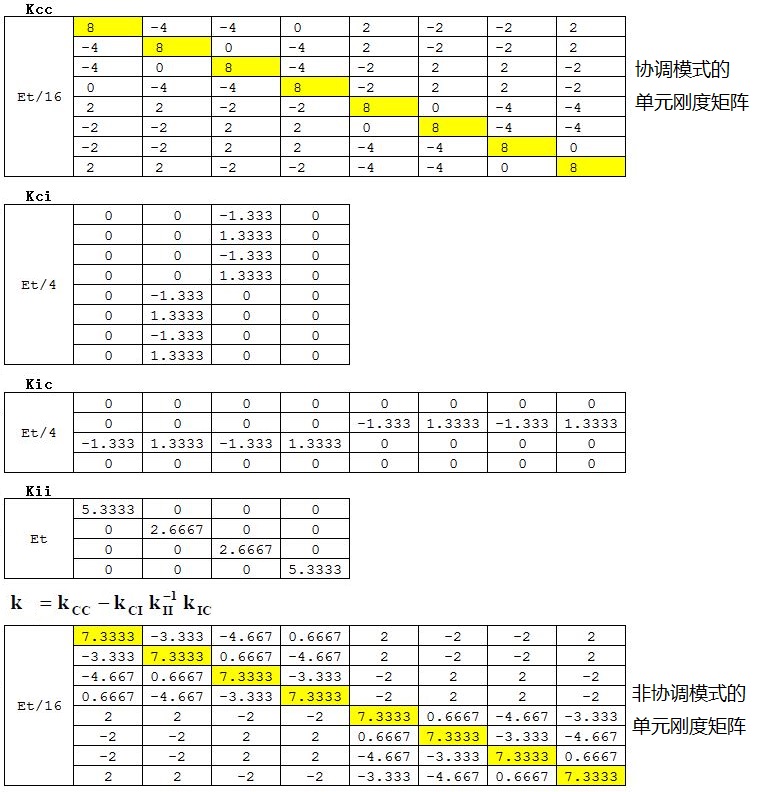
将各个单元的刚度矩阵进行组装得到总体刚度矩阵K,再根据U=K-1R,计算出各个节点的位移。
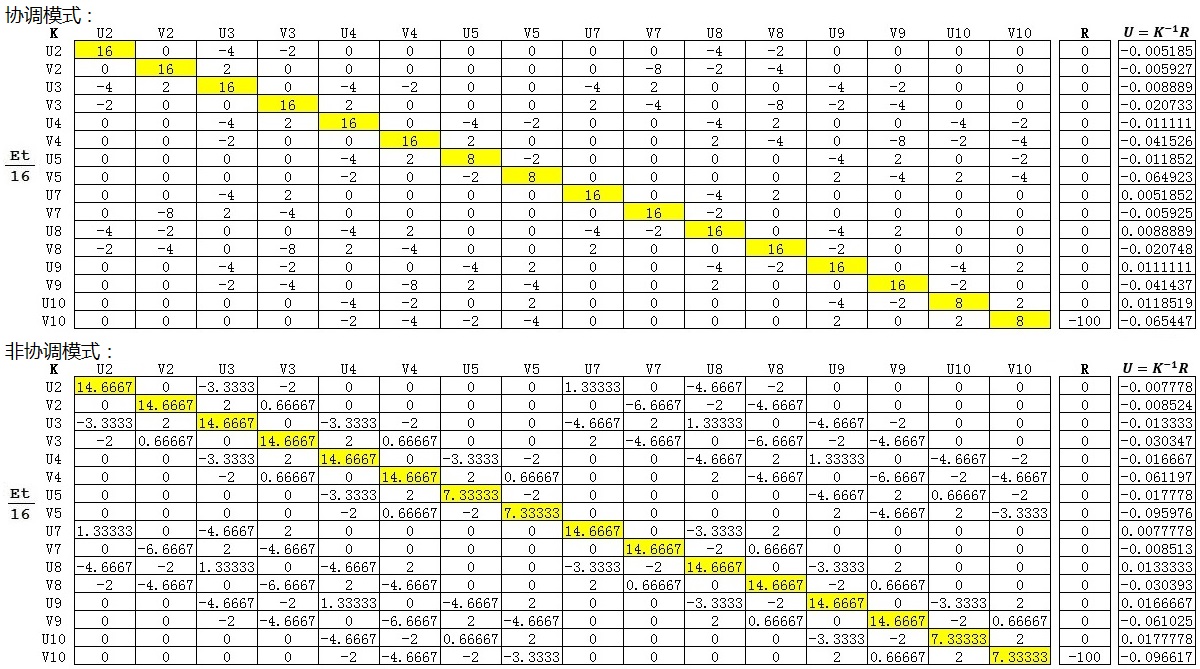
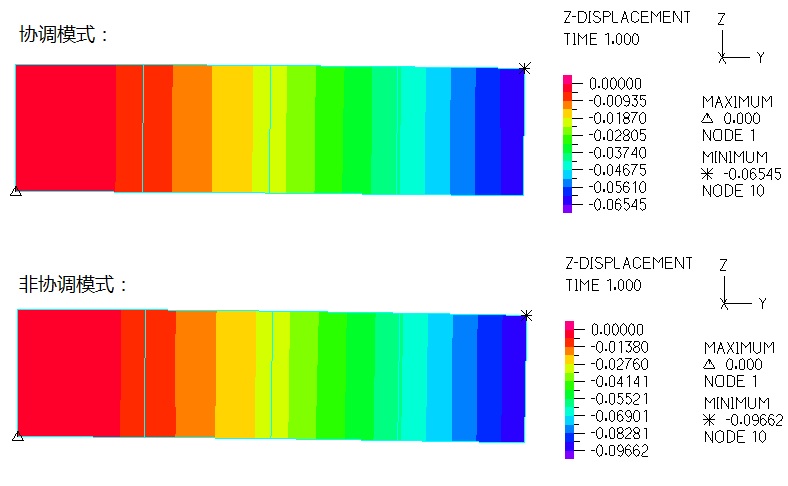
协调模式和非协调模式,载荷作用点在竖直方向的位移(V10)分别为-0.06545和-0.09662。两种情况得到的结果,与下图Adina软件的分析结果一致。
Reference:
- Finite Element Procedures by Klaus-Jürgen Bathe 轩建平 译
- A First Course in Finite Elements by Jacob Fish & Ted Belytschko