材料力学性能(1)拉伸试验
简介
材料学,通过试验来研究材料的力学性能。试验的结果取决于试件的形状、尺寸、装夹方式以及测试方法。因此需要统一试验流程和标准。拉伸试验,作为测试材料强度的基础试验,被广泛接受。
最常用的是单轴拉伸试验(沿中心轴线施加载荷),以规定的速率均匀地拉伸试样,记录拉力和伸长量。推导出应力-应变曲线、屈服强度、抗拉强度和断裂伸长率等材料参数。此外,还有双轴拉伸试验。

应力和应变
为了方便对不同尺寸试件的力学性能进行对比,将单位面积上受到的力作为统一的量化指标,即“应力”(Stress σ)。
应力(σ)等于力(F)除以试件初始横截面积(A0),与压强的的单位(Pa)相同。不同的是:压强一般用于描述物体表面单位面积上受到外力的大小,而应力是指物体内部某个微元单位截面积上受到内力的大小。
在拉压试验中,试件会被拉长或者缩短,伸长量用△L表示(负值代表缩短)。为了方便对不同长度的试件进行对比,我们将伸长量(△L)除以试件初始长度(L0),记为“应变”(Strain ε)。

试验过程中,随着拉力增加,记录应力和应变的数据,绘制成曲线,即“应力-应变曲线”。金属的应力-应变曲线,与其成分、热处理状态、已产生的塑性变形、应变率、温度以及应力状态都有关系。
用于描述应力-应变曲线的材料参数有:屈服强度、抗拉强度、断裂伸长率以及断面收缩率。前两个参数表征强度,后两个参数表征延展性。
在弹性变形阶段,应力与应变成正比,两者是线性关系,载荷撤销后,试件可以恢复到初始形状。载荷继续增加,使材料应力超过屈服强度,试件会产生不可恢复的塑性变形,载荷撤销后,试件不能完全恢复到初始形状。(弹性变形可以恢复,塑性变形不能恢复)。
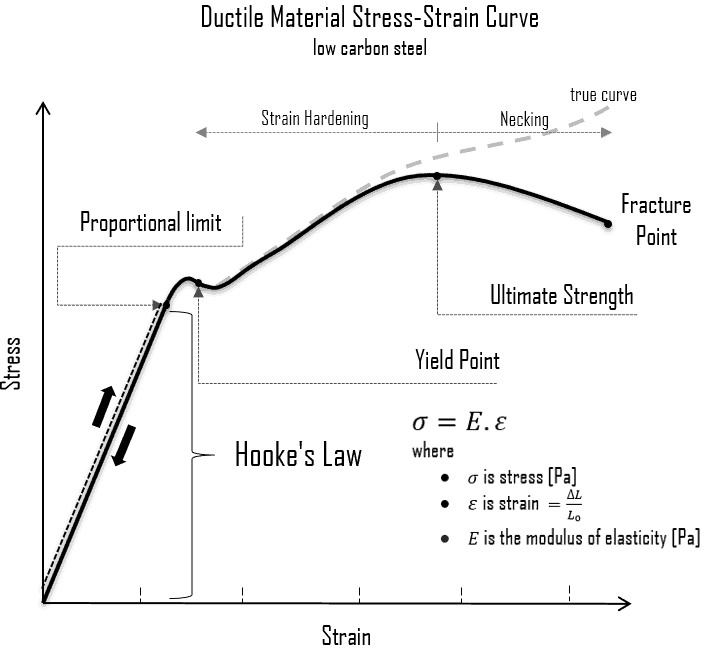
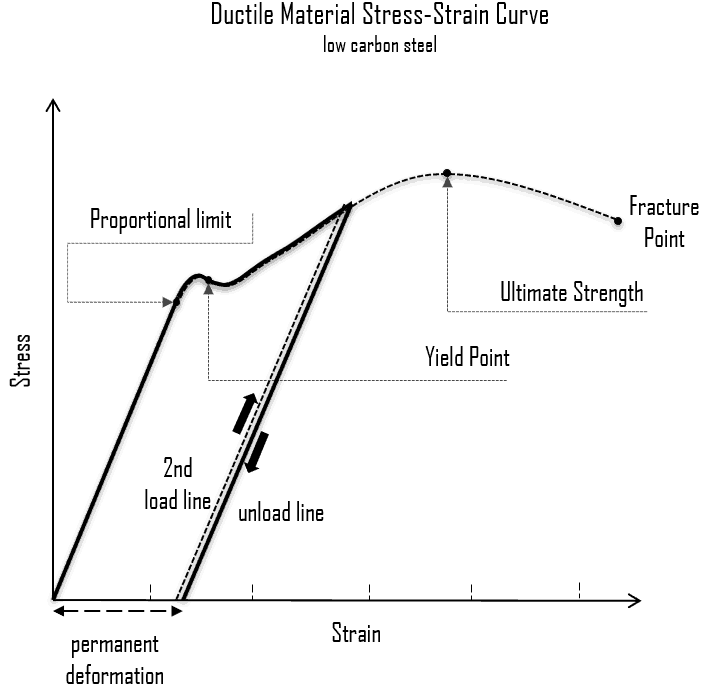
对已经发生塑性变形的试件,撤销载荷后重新施加载荷,需要施加比之前更大的载荷,才能使材料产生更多的塑性变形。这种现象,称为金属材料的“应变硬化”。在塑性变形过程中,试件的体积保持不变:A·L = A0·L0,随着拉伸长度L增加,横截面A会减小。
正应变与切应变
应变等于变形量除以初始长度,用于描述材料的相对变形。
当力的方向与截面方向垂直时,截面上产生正应力;
当力的方向与截面方向平行时,截面上产生切应力。
正应变描述垂直于截面方向的相对变形;切应变描述平行于截面方向的相对变形。

泊松比
Poisson's ratio is the ratio of transverse contraction strain to longitudinal extension strain in the direction of stretching force. Tensile deformation is considered positive and compressive deformation is considered negative. The definition of Poisson's ratio contains a minus sign so that normal materials have a positive ratio.
翻译一下:泊松比,是横向收缩应变与载荷方向的轴向伸长应变的比值。拉伸应变是正值,压缩应变是负值。因此,泊松比的定义中,包含了一个负号,以使常见材料的泊松比为正。
写成公式就是:ν = - εtrans / εlongitudinal
常见的材料,轴向受到拉伸时,横向会缩小,即:轴向应变是正数时,横向应变是负数。如果直接把泊松比定义为横向应变与轴向应变之比,那么常见材料的泊松比就是一个负数。为了让常见材料的泊松比为正数,所以定义中增加一个负号。

泊松比为负的材料,受到拉伸时,横向反而增大。这种材料也是存在的,比如某些特殊的泡沫材料。



下表列出了一些材料的泊松比:
